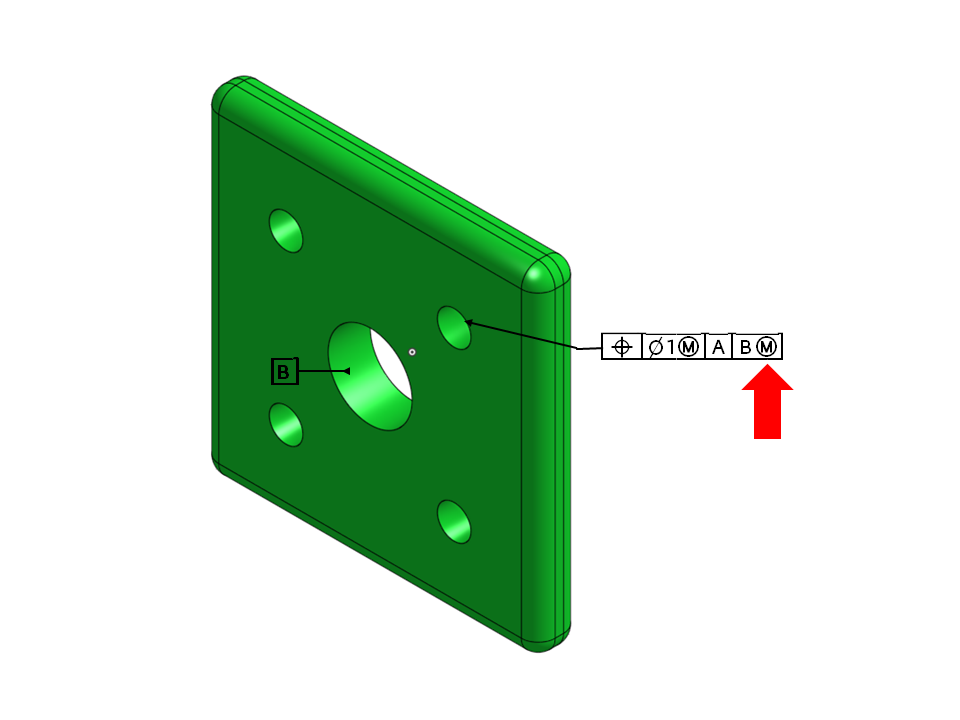
図 1.この図のB(M)という注釈は、データムBに適用される最大実体境界を表示
この記事の目的は、幾何公差における最大実体境界(MMB)の概念を説明することです。最大実体境界の概念は、図1(注釈 B(M))に示すように、基準面に最大実体状態を使用することです。その主な用途は、部品の組み立て条件を緩和することです。
最大実体境界の概念を完全に理解するには、より基本的な概念であるデータム基準枠(DRF)(図2)を理解する必要があります。
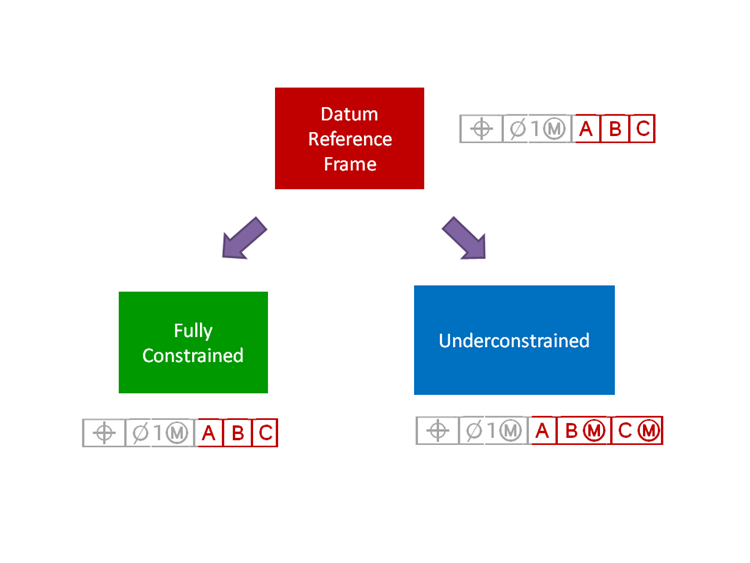
図2. 幾何公差におけるデータム基準枠の概念
データム基準枠:製品を定義する3次元の直交座標系。寸法と公差はすべてデータム基準枠に由来します。
完全拘束:完全拘束の状態では、評価対象の部品が完全に固定化され、部品のすべての自由度が制限されます。部品を物理的に固定するには、チャック、マンドレル、万力などを実用データム形体として基準面に使用できます。
制約不足:制約が不十分な場合、部品は条件によって移動可能です。これについては後で詳しく説明しますが、重要な点は、部品にはある程度の自由があり完全に固定されているわけではないということです。実体状態が割り当てられたデータムを持つ部品、またはデータムが3個未満の場合は、一般に制約条件が不足していると考えられます。
制約不足の条件下でデータム基準枠を定義する理由:MMBコンセプトの最大の利点は組み立てが容易になることです。MMBが許す限り、部品はガタガタと揺れたり、動いたりでき、これにより公差内に収まることとなります。
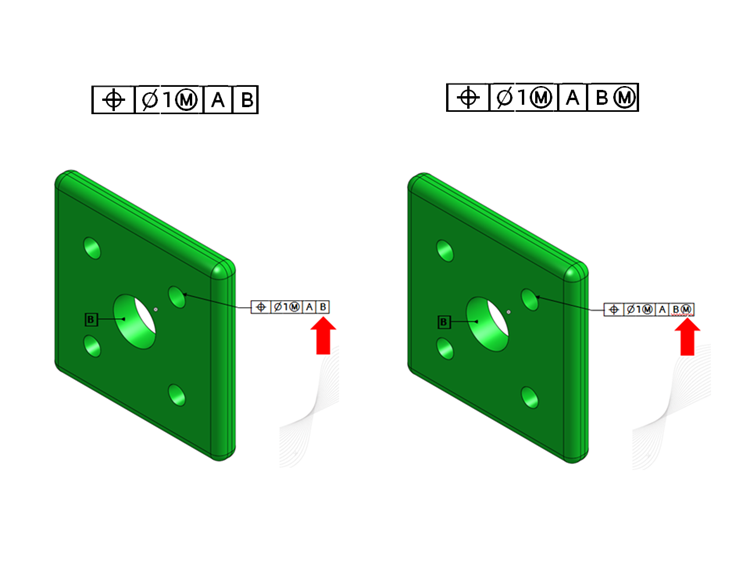
図 3. 両方の部品の制約が不十分。違いは、右側の部品には実体境界状態の2次データムがあること
制約不足(図3、左)
両方のデータムがRMB(実体境界を使わない)で定義されます。この部品はまだ制約不足です。仕様では回転を止めるためのデータムCがないため、Bを中心に回転します(スロットまたはキー溝があった可能性があります)。
データムBの制約不足 + 最大実体境界状態(図3、右)
今回はデータムBがMMBで定義されています。これにより、データムBの軸を中心に回転と平行移動が可能になります。
この状態の効果はどのようなものでしょうか。図4は、制約不足の部品とそれに対応するゲージを示しています。
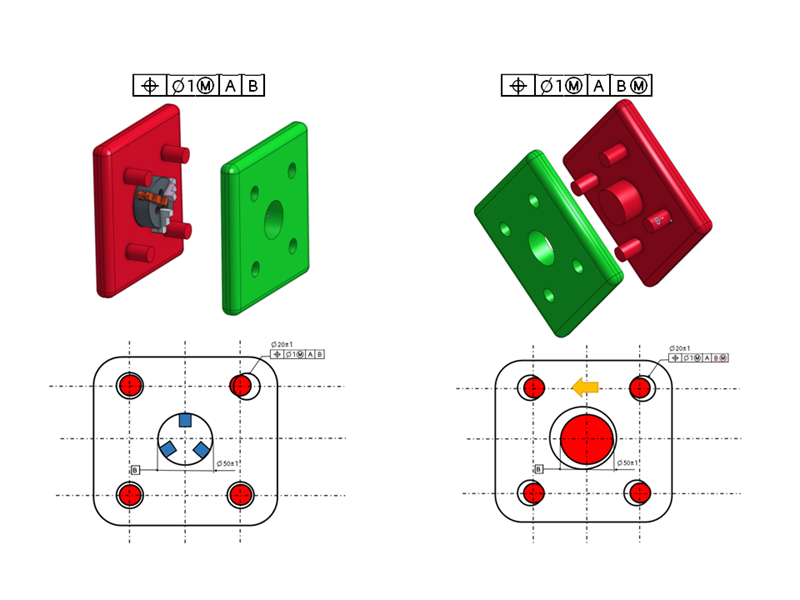
図4. 制約不足の部品と対応するゲージ
制約不足(図4、左)
データムBのチャックを使用して部品を固定すると、部品はデータムBに対して完全に固定されます。
ここで、1つの穴が平行移動の位置で誤った配置にあると想像してみましょう(図4、左下)。この状態では部品を平行移動させることが許されていないため、私たちにできることは何もありません。公差を外れているため、部品は検査に合格しません。
チャックは移動中に部品をしっかりと保持しているので、この自由度では穴のパターンがずれることはありません(部品が小刻みに動く余地はありません)。
Bの制約不足+実体状態(図4、右)
実体状態の制約不足の部品では、Bの固定ゲージを使用できます(図4、右下)。このゲージの寸法はデータムBのMMBによって定義されます。これは、データムBの可能な限り最小の穴径に対応します。
データムBの穴がMMBよりも低い状態で製造され、サイズが大きくなると、可動性が大きくなります(図4、右下)。この余分な可動性によって、検査に余裕を持たせることができ、その部品を合格させることができるのです。
まとめ
最大実体境界条件の概念は、より簡単な組み立て条件を可能にするため、非常に有用です。基準面がそのMMBから離れると、位置度公差が通るようにシフトを許容することができます。今後の記事では、具体的な用途の事例についてさらに詳しく説明します。