この記事では、幾何公差で平面度を評価する複数の方法を取り上げ、どれが最適なアプローチであるかを判断します。
平面度は、概念的にはシンプルな幾何公差です。ASME Y14.5規格によれば、これは「表面がその間に位置しなければならない2つの平行な平面によって定義される公差を指定」します。
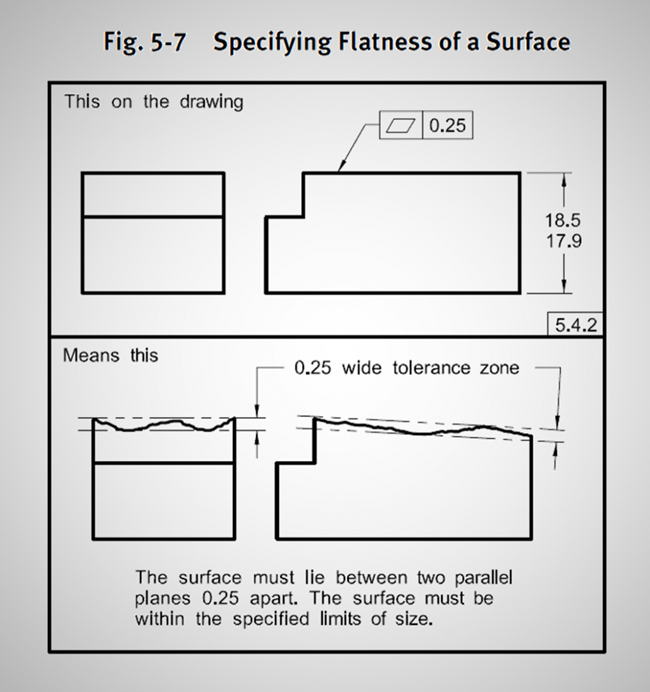
図1. ASME幾何公差平面度の例
図1は、この概念を非常によく示しています。上の図は、平面度の公差が0.25の図面を示しています。規格によると、これは上面が完全に最大0.25の間隔の2つの平行な平面の間になければならないことを意味します。平行な2つの平面の間に、可能な限りきっちりと表面を挟み込むイメージで、0.25より近づけることができれば公差はクリアできます。図1の下の図でわかるように、2つの平行な平面は必ずしも何かに沿っているわけではないことに注意することが重要です。
ハイトゲージを使用した平面度の評価

図2. ハイトゲージで平面度を評価
応用として、物理的に平面度を測定する1つの方法は、図2に見られるように、ハイトゲージを使用することです。ハイトゲージを正しく使用するには、まず測定する部品を高さ調節可能な3本の支柱の上に置きます。次に、ハイトゲージを表面に沿って動かし、針の振幅を確認します。測定作業者は、針の振幅が最小になるように3つの支柱を調整します。平面の配向を調整して、理論上最小の二平面を導き出します。ご想像のとおり、この方法には多大な忍耐と訓練が必要です。
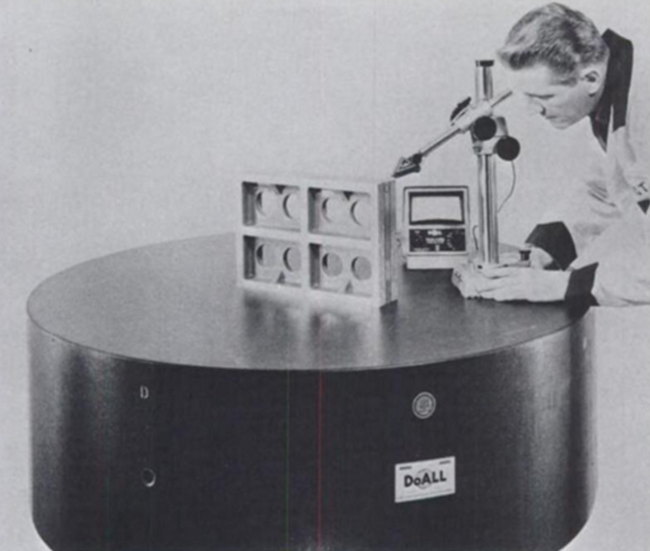
図3. 部品を測定テーブルに直接置いた状態でハイトゲージを使用すると、偽陰性になる可能性がある
ハイトゲージを使用して平面度を評価する、より一般的な方法は、部品を測定テーブルの上に直接置くことです(図3)。しかし、針の振幅を最小限に抑えるように部品の向きを調整できないと、基本的にテーブルに基づいて平行度を評価することになり、これは最適とは言えません。3つの支柱を使用するよりもはるか速く測定できますが、この方法では偽陰性になる可能性があることに注意することが重要です。この評価に合格した部品は常に正しいものとみなされますが、良品が費用のかかる再加工のために返送されることのないように、不合格となった部品は別の方法で評価する必要があります。
デジタルでの平面度の評価
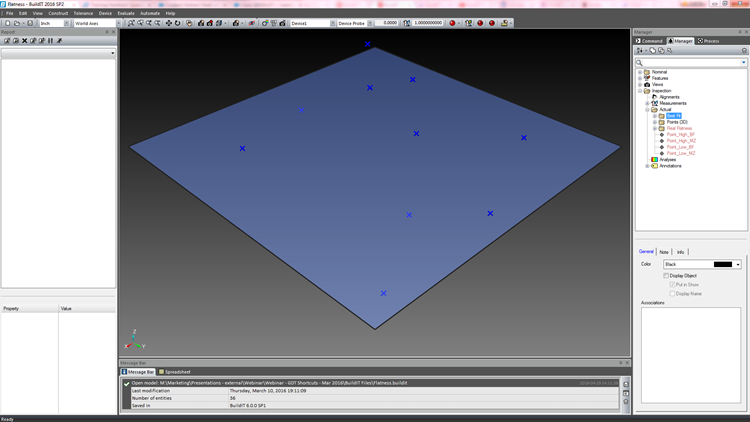
図4. 平面度の公差が0.57の表面
それでは例を見てみましょう。平面度の公差が0.57の表面があります(図4)。デジタル領域では、三次元測定機(ポータブルまたはその他)を使用して測定を行う場合、ソフトウェアには平面度を評価する2つの方法(ベストフィットまたは最小領域)があります。
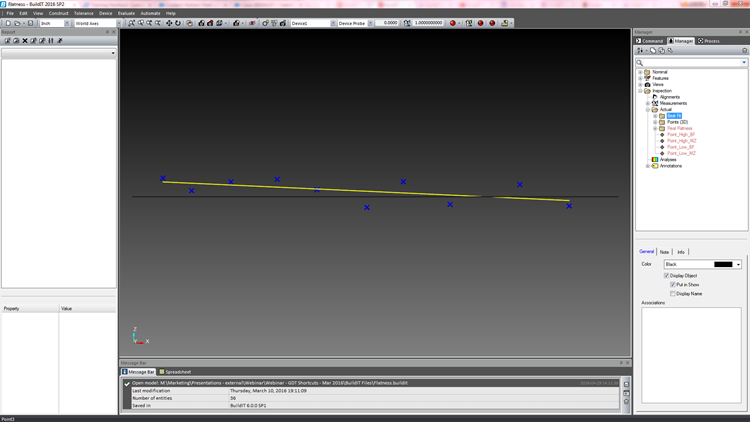
図5. 点群から計算したベストフィット平面
ベストフィットは、RMS平面とも呼ばれ、点群を通して平面を最適にフィットさせる方程式で、異常値の影響を最小限に抑えながら平均を求めます(図5)。次に、アルゴリズムはフィット面の上下の最大偏差を計算し、その偏差を通る2つの平行な理論平面を作成し、それらの間の距離を計算します。図6に示すように、これは公差を評価するために使用されます。
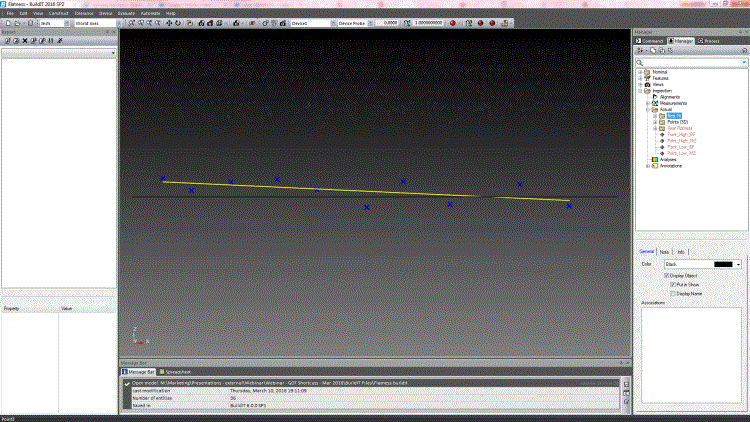
図6. 0.6121の偏差を持つベストフィット平面。アルゴリズムは、Point_High_BFおよびPoint_Low_BFとマークされたフィット平面の上下の最大偏差を計算します。これらの偏差を通る2つの平行な理論平面(灰色)を作成し、それらの間の距離を計算します
調節可能な支柱のないハイトゲージを使用するのと同様に、ベストフィットは幾何公差において平面度を評価する方法として最適とは言えない方法です。というのも偽陰性になりやすいからです。つまり、平面度が正しく評価されていれば合格するはずの部品が、不合格になる可能性があるということです。この例では、この平面の平面度公差は0.57です。平面度を評価するベストフィット法を使用すると、偏差は0.6125となり、部品は評価不合格となります。これは偽陰性です。なぜなら、アルゴリズムによって作成されるベストフィット平面が、幾何公差ASME規格に従って表面が置かれるべき2つの理想的な平面と必ずしも平行ではないためです。ベストフィット平面の向きは固定されているため、アルゴリズムが2平面を調整して偏差を最小限に抑えることができなくなります。この方法は、堅牢で高速であり、計算の負担が少ないため、歴史的に測定ソフトウェアで使用されてきました。しかし、現代のコンピューティング能力により、最小領域というはるかに優れた方法を使用できるようになりました。
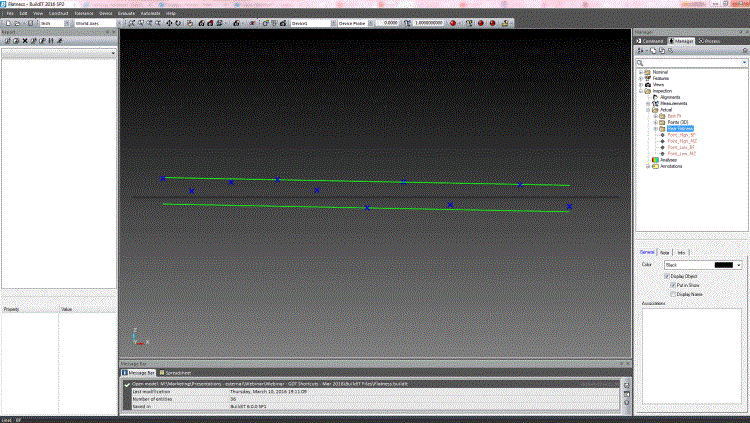
図 7. 偏差が0.5419の最小領域平面度評価。
幾何公差で平面度を評価する最小領域法は、 ASME規格に最も近いため、最も精度の良い方法です。上の図7では、点をできるだけしっかりと挟むために、ソフトウェアが2つの理論上の平行な平面を作成していることがわかります(緑色で表示)。上記と同じサンプル面を使うと、2つの平面間の距離は0.5419です。これは0.57の公差に合格します。
下の図8は、ベストフィット法と最小領域法で平面度を評価する際の2平面間の向きの違いを示しています。
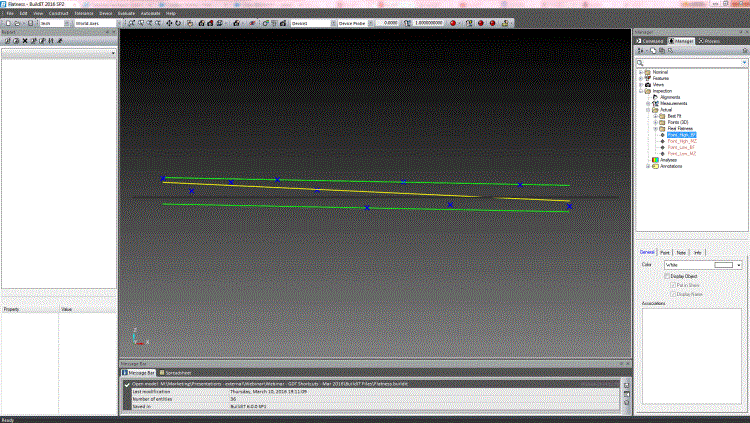
図8. ベストフィットと最小領域の平面度評価を比較すると、2平面の計算に使用した平面の向きの違いがわかる。この例では、それぞれの計算で異なる高点が選択されている。
結論:幾何公差において平面度はどのように評価すべきか?
ポータブル3次元測定器や高度な3次元測定ソフトウェアを用いて幾何公差を評価するデジタル手法の出現により、最適でない方法や時間のかかる方法を使用し続ける理由はなくなりました。ベストフィットを使用して平面度を評価する場合、速度やリソース面で大きなメリットはありません。最小領域は、規格に忠実であり、高価な再加工のために良品を返送する可能性がないという利点もあるため、最適な方法です。
